(Продолжение. Начало в №3)
Символьные преобразования
Преобразование рациональных выражений
Значительная часть функций системы предназначена для преобразования рациональных выражений. Рациональным называется выражение, которое состоит только из арифметических операторов и оператора возведения в натуральную степень. Элементы такого выражения могут также содержать не арифметические и не степенные функции. В этом случае такие элементы считаются атомарными, то есть неделимыми и не преобразуемыми.
Функции, которые работают с рациональными выражениями, описаны в разделе документации "Polynomials", поскольку рациональные функции, с математической точки зрения, рассматриваются как расширение многочленов (полиномов), примерно так же, как рациональные числа считаются расширением целых (многочлены, кстати, тоже иногда называют целыми функциями, хотя общий математический смысл этого термина шире).
Имена всех функций системы для обработки рациональных выражений содержат текст "rat" (от английского rational).
Функция rat
Эта функция преобразует рациональное выражение к так называемой канонической форме (Canonical Rational Expression, CRE). То есть она раскрывает все скобки, приводит все к общему знаменателю, суммирует и сокращает; кроме того, приводит все числа в конечной десятичной записи к рациональным.
Синтаксис функции:
rat(математическое выражение)
Например:
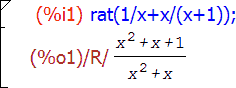
Во время использования сложных математических выражений запись функции удобно производить за два этапа:
- Ввести математическое выражение. После его ввода в текстовом виде оно будет отображаться в графическом виде, что дает возможность проверить корректность его ввода.
- Ввести функцию, аргументом которой будет ссылка на ячейку, содержащую математическое выражение, то есть на последнюю ячейку.
Пример:
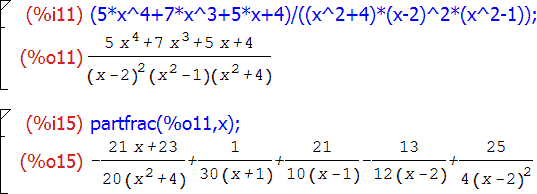
Следует заметил, что атомарные элементы, то есть символы и числа в канонической форме рационального выражения, в Maxima имеют другое внутреннее представление. При этом визуально для пользователя каноническая форма от общей ничем не отличается. Но один достаточно интересный момент здесь есть: если каноническая форма рационального выражения используется в других рациональных выражениях, то последние также автоматически приводятся к канонической форме. Это удобно, если нужно последовательно выполнить большое количество рациональных преобразований. В этом случае можно, один раз вызвав функцию rat(), ссылаться на предыдущие ячейки и, благодаря этому, видеть на каждом шагу полученное выражение в канонической форме. Если на каком-то этапе такое поведение системы будет мешать, то можно преобразовать выражение из канонической к общей формы с помощью функции ratdisrep (выражение). Кроме того, каноническая форма автоматически "отменяется" в случае любых нерациональных преобразований:
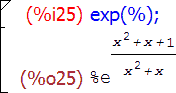
Несмотря на то, что в ячейке (%o2) было выражение в канонической форме, ячейка вывода (%o3) содержит выражение общего вида, поскольку значение в ячейке не является рациональным.
Разложение биномов
Для этого используют функцию ratexpand(выражение). Она раскрывает скобки в рациональном выражении (один из смыслов слова expand и является "раскрыть скобки"). Здесь также действует системная опция keepfloat. На результат работы функции влияет системная опция ratdenomdivide. По умолчанию она имеет значение "true". В этом случае каждая дробь, в которой числитель является суммой, раскладывается на сумму дробей с одинаковым знаменателем. Если же присвоить этой опции значения "false", то тогда все дроби с одинаковым знаменателем будут объединены в одну дробь с числителем в виде суммы числителей начальных дробей.
Пример:

То есть внешне результат в этом случае будет выглядеть почти так же, как и в функции rat(); к тому же единственная заметная для пользователя разница обнаруживается только в рациональных выражениях от нескольких переменных (или разных иррациональных выражениях). Заключается эта разница в том, что после ratexpand() и в числителе, и в знаменателе дроби все скобки будут раскрыты, в случае же rat() слагаемые, где имеются, например, две переменные, будут сгруппированы, и одна из них будет вынесена за скобки (в документации такая форма записи называется "рекурсивной" (recursive)).
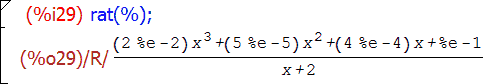
Для разложения биномов применяется также функция expand. Между ней и функцией ratexpand существуют несколько отличий:
- expand раскрывает скобки на всех уровнях вложенности, а ratexpand раскрывает рациональное выражение только первого уровня, при этом подвыражения, которые не являются рациональными, не обрабатываются;
- ratexpand приводит дроби-слагаемые к общему знаменателю, а expand этого не делает;
- на expand не влияет системная опция ratdenomdivide;
- expand не преобразует в рациональные числа конечную десятичную запись независимо от значения системной опции keepfloat.
Синтаксис функции:
expand(выражение)
Пример:
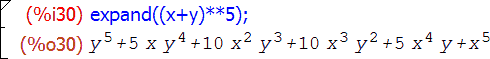
Упрощение выражений
Для упрощения рациональных выражений применяется функция ratsimp(выражение). Она упрощает выражение за счет рациональных преобразований. Но, в отличие от других функций, для обработки рациональных выражений, она работает также "вглубь", то есть иррациональные части выражения не рассматриваются как атомарные, а упрощаются:
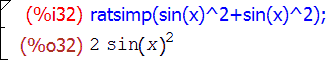
Функция ratsimp является мощным и в то же время быстрым механизмом упрощения. Но все же он не является достаточным, поскольку действия, которые можно упростить в разнообразных математических выражениях, не ограничиваются рациональными. Поэтому основное достоинство этой функции - это скорость. А для более серьезных упрощений существует расширенный вариант - fullratsimp(выражение). Эта функция последовательно применяет к выражению функцию ratsimp, а также некоторые нерациональные преобразования и повторяет эти действия в цикле до тех пор, пока выражение не перестанет в процессе преобразования изменяться. За счет этого функция работает несколько медленнее, чем ratsimp, зато дает более надежный результат, а к некоторым выражениям, которые она может упростить сразу, ratsimp пришлось бы применять несколько раз, а иногда она и вообще бы не справилась с заданием.
Разложение выражения на множители
Для этого используется функция factor. При этом если аргументом функции будет целое число, то функция раскладывает его на простые множители; если же аргументом является рациональное число, то на множители раскладываются его числитель и знаменатель:

Нахождение наибольшего общего делителя многочленов
С этой целью применяется функция gcd, аргументом которой является выражение-многочлен:
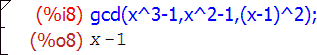
Преобразование рациональной дроби в простых дроби
Применяется функция partfrac. Она имеет два аргумента: математическое выражение и переменная, по которой происходит преобразование. Например:
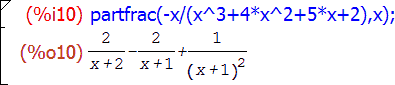
Решение задач линейной алгебры
Функции для нахождения числовых характеристик матриц
| transpose(M) | Транспонирование матрицы M |
| matrix_size(M) | Определение количества столбцов и строк матрицы |
| rank(M) | Определение ранга матрицы |
| mattrace(M) | Определение следа (суммы диагональных элементов) квадратной матрицы* |
| determinant(М) | Вычисление определителя (детерминанта) квадратной матрицы |
| invert(M) | Вычисление матрицы, обратной к М |
| * приложению предшествует загрузка пакета для работы с матрицами: load ("nchrpl"). | |
Решение уравнений
Для решения уравнений или систем уравнений используется функция solve. В самом простом виде функция solve имеет только один аргумент: отдельное уравнение или систему уравнений. При этом аргумент можно представить как в форме выражения, например, x2-1, так и в форме уравнения x2=1. Возвращает функция найденные корни:
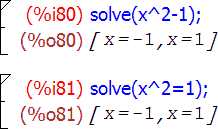
Здесь [x=-1, x=1] являются численными вариантами решения, то есть множеством возможных значений х.
Если уравнение не имеет решения на множестве вещественных чисел (), то Maxima ищет решения среди комплексных чисел:
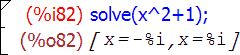
Система способна одновременно находить как численные корни, так и комплексные с помощью тот же функции solve:
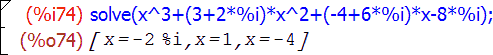
Если корни уравнения не определяются в радикалах или их выражение достаточно громоздко, то Maxima представляет результат так:
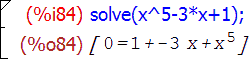
Для решения систем уравнений аргумент функции solve записывается в виде множества уравнений, то есть они заключаются в квадратные скобки и отделяются один от другого запятой.
Пример решения системы уравнений 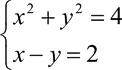 :
:
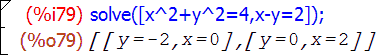
В следующем примере функция solve используется для решения системы из трех уравнений с тремя неизвестными:
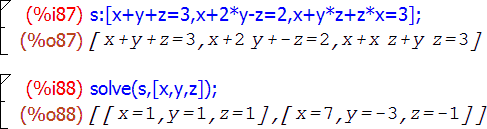
Еще проще решать уравнение с помощью панели общих математических действий (General Math). Для этого на панели следует щелкнуть кнопку "Решить" а потом в окне "Решить" ввести математическое выражение в поле "Equation" (Выражение). Отметим, что решение по умолчанию осуществляется относительно переменной х, поэтому имя переменной в выражении также должно быть х.
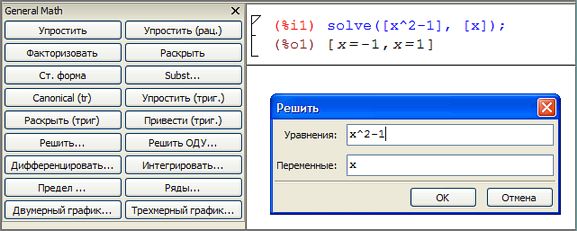
Решать неравенства и системы неравенств Maxima не способна.
Валерий ФЕТИСОВ






















Комментарии
Способна:
load("solve_rat_ineq");Не знал... Спасибо, взял "на вооружение"