Рассмотрим упрощённую игру в покер, в которой принимают участие 2 игроков (упрощённый аналог игры хедзап). Игра состоит из 100 конов. В каждом коне игрокам выдаётся по 2 карты из колоды с 52 картами (4 масти от двойки до туза) так, чтобы каждый игрок увидел свои карты, но не видел карт противника. После этого игроки записывают в своих блокнотах ставки, которыми являются числа от 0 до 99. Каждому игроку неизвестна ставка его противника. Далее из колоды извлекается и показывается 5 карт. Игрок, сумевший составить более высокую комбинацию из 5 карт с использованием личных 2 и общих 5 карт, назначается победителем кона.

Игрок, проигравший в коне, ставит перед своей ставкой в блокноте знак "минус". После этого карты перемешиваются и начинается следующий кон, в котором игроки будут записывать свои ставки под ставкой предыдущего кона. По завершении игры выигрыш игроков складывается из суммы записей, сделанных в их блокнотах. Далее мы увидим, что данная игра не является антагонистической (то есть выигрыш одного игрока в общем случае не равен проигрышу его противника), а также имеет положительную цену для отдельного игрока, то есть обеспечивает при оптимальной стратегии его положительный выигрыш. Дальнейшее повествование будет посвящено определению оптимальной стратегии данной игры.

Основные ситуации. Анализ данной игры был осуществлён на компьютере при использовании метода Монте-Карло. Для этого потребовалось выделить основные сочетания 2 карт, которые могли оказаться у заданного игрока. Далее пронумеруем карты одной масти числами от 1 до 13. Таким образом, отметим, что 2 карты игрока могли оказаться одной масти, откуда имеется  соответствующих сочетаний. Рассмотрим теперь случай, когда карты имеют разную масть. В этом случае имеется 13 сочетаний из одинаковых карт и  сочетания разных карт. Итого - 78∙2+13 = 169 различных ситуаций, с которыми может столкнуться игрок. Целью компьютерного эксперимента было определение вероятностей выигрыша в рассматриваемой игре для каждой найденной ситуации. Для этого компьютер воспроизводил 10000 случайных игр (отдельных конов) для каждой из 169 комбинаций, отмечая, сколько раз данная комбинация приводит к выигрышу (в терминах обычной игры в покер компьютер определял всевозможные значения эквити на префлопе).

Определение весовой функции. Основной тактической проблемой при постановке эксперимента было сравнение двух комбинаций из 5 карт, для чего потребовалось ввести функцию веса комбинации. Для описания функции веса обратимся к комбинациям игры в покер в порядке возрастанию их приоритета:

1. Старшая карта (комбинация не соответствует ни одному из перечисляемых далее типов, основная её оценка осуществляется по карте с наибольшим значением).
2. Пара. 2 карты одного значения.
3. Две пары. 2 карты одного значения и 2 карты - другого.
4. Сет. 3 карты одинакового значения.
5. Стрит. 5 карт, идущих по убыванию (сюда относится и сочетание 4,3,2,1,13).
6. Флеш. 5 карт одинаковой масти.
7. Фулл. 3 карты одного значения и 2 карты - другого.
8. Каре. 4 карты одинакового значения.       
9. Роял и стрит флеш. Карты одной масти, идущие по убыванию (сюда также относится сочетание 4,3,2,1,13).

Следует отметить, что по правилам игры в покер 2 комбинации, имеющие одинаковый из 9 указанных типов рассматриваются "по старшинству", а также по значению карт (киккеров), которые не определяют в данной комбинации её тип. Этот принцип мы рассмотрим подробнее, непосредственно определяя весовую функцию комбинаций P, для чего последовательно рассмотрим приведённые типы.

1. Старшая карта. Упорядочим комбинацию по убыванию значений карт и присвоим ей вес a[1]∙100000000+a[2]∙1000000+a[3]∙10000+a[4]∙100+a[5], где a[1] и a[5] - соответственно наибольшее и наименьшее значение в комбинации. Таким образом, "более старшая" комбинация данного типа будет иметь больший вес - например, наборам 3,12,1,4,5 и 8,11,10,9,6 будут соответствовать веса 1205040301 и 1110090806.

2.  Пара. Положим, что среди карт a[1], a[2], a[3], a[4] и a[5] данный тип комбинации был составлен картами a[2] и a[4], при этом при сортировке других карт по убыванию мы получим ряд a[1], a[5], a[3]. Припишем весовой функции значение  a[2]∙100000000+a[4]∙1000000+a[1]∙10000+a[5]∙100+a[3] и умножим его на 10², чтобы обеспечить минимальному весу комбинации данного типа (9‑значное число) значение, большее максимального значения веса среди комбинаций прошлого типа (10-значное число)

3. Две пары. Положим, что среди карт a[1], a[2], a[3], a[4] и a[5] "пары" соответствуют картам a[2], a[4] и a[1], a[5], причём a[2] < a[1]. Тогда вес  комбинации будет получен умножением a[1]∙100000000+a[5]∙1000000+a[2]∙10000+a[4]∙100+a[3] на 10⁴.

4. Сет. Для определения веса сета разместим после 3 одинаковых карт отсортированные по убыванию остальные карты, после чего вновь выполним описанную в предыдущих типах процедуру с умножении на 10⁶.

5. Стрит. Для определения веса комбинации стрит достаточно отсортировать все карты по убыванию, рассмотрев отдельно ситуацию 4,3,2,1,13. После этого выполняется процедура присваивания веса при умножении на 10⁸.

6. Флеш. При определении веса выполняем проверку на одинаковое значение масти, сортируем карту по убыванию и присваиваем вес вышеуказанным способом с умножением на 10¹⁰.

7. Фулл. Разместим в начале ряда 3, а затем - 2 одинаковые по значению карты и припишем вес с умножением на 10¹².

8. Каре. Разместим в начале ряда 4 одинаковые по значению карты, добавив оставшуюся карту в конец ряда. Припишем вес с умножением на 10¹⁴.

9. Роял и стрит флеш. Проверим, что все карты имеют одинаковую масть, после чего выполним процедуру, аналогичную ситуации стрит с умножением на 10¹⁶.

Суть дальнейшей работы компьютера заключалась в определении максимального веса среди всевозможных комбинаций по 5 карт из 2 заданных карт игрока и 5 открытых карт с последующим сравнением этого значения с аналогичным значением веса у противника. Для каждой из 169 возможных пар было поставлено 10000 экспериментов-игр, в результате которых отмечались те случаи, когда максимальный вес комбинации игрока оказывался больше максимального веса комбинации противника, то есть - число побед.

Результаты эксперимента. Результаты, полученные в эксперименте, были занесены в 2 таблицы, в которых отображены проценты выигрышей при всевозможных парах карт. Первая таблица соответствует картам одной масти, вторая - картам разной масти, соответствующий процент выигрыша в обеих таблицах размещён на пересечении значений 2 карт:

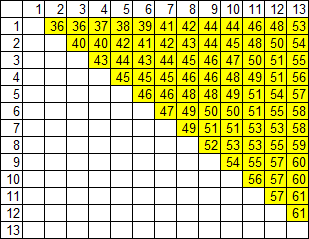
Таблица 1. Процент выигрышей для пар карт одинаковой масти

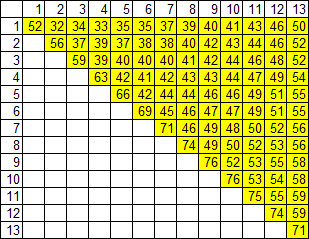
Таблица 2. Процент выигрышей для пар карт разной масти

Определение оптимальной стратегии. Для определения оптимальной стратегии, позволяющей максимизировать выигрыш игрока по завершении 100 конов игры, отметим, что каждая из игр не зависит от остальных, откуда максимум выигрыша от всей игры достигается при максимальном выигрыше каждой из отдельных игр. Положим, что P - вероятность выигрыша в данной игре, определяемая по полученным выше таблицам (отношением указанного числа к 100) в соответствии с 2 картами игрока до того, как он сделал ставку. Тогда выигрыш S данной игры определяется её ставкой C и значением P: S = CP-C(1-P) = C(2P-1). Таким образом, в зависимости от того, положительно или нет - значение 2P-1 (то есть выполнено или нет - отношение P > 0,5), выигрыш игры будет представлен соответственно прямыми с положительным и отрицательным наклоном. Таким образом, при P > 0,5 максимальный выигрыш соответствует максимальному значению C, то есть 99. Если P ≤ 0,5, то максимум выигрыша соответствует минимальному значению ставки - 0. Таким образом, оптимальная стратегия игры заключается в том, чтобы совершать максимальную ставку, если вероятность выигрыша с заданными 2 картами больше 0,5, и при этом делать минимальную ставку для противного случая.

Определение цены игры. Отметим, что сочетания 2 карт, рассмотренные в таблицах, встречаются с различной частотой. Так, выбрать соответствующую комбинацию для карт одной масти мы можем 4 способами. Выбор 2 одинаковых карт разных мастей осуществляется  способами. Выбор 2 разных карт разных мастей осуществляется 4∙3 = 12 способами. Таким образом, общее количество ситуаций игрока равно 4∙78+6∙13+12∙78 = 1326. Обозначая частоту выигрыша как N и осуществляя суммирование по всем случаям с P > 0,5, найдём цену игры:

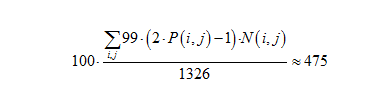
Отметим, что интуитивная стратегия осуществления ставки пропорционально вероятности выигрыша не является оптимальной и в данной игре приводит к отрицательному выигрышу (суммирование в данном случае ведётся при всех комбинациях):

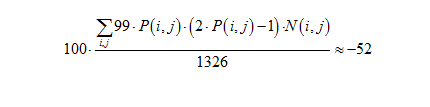
Отметим в заключение, что рассмотренная игра не является антагонистической, поскольку выигрыш игрока полностью обусловлен его поведением и не зависит от поведения противника. Так, при оптимальной стратегии оба игрока могут рассчитывать на одинаковый выигрыш, соответствующий цене данной игры.

Эльмар Гусейнов